Matlab FIR Filter
This content relates to a deprecated version of Mbed
Mbed 2 is now deprecated. For the latest version please see the Mbed OS documentation.
Design a simple set of filter coefficients, apply it to a test signal and visualise results
Test Signal¶
320 samples at 48kHz for a sum of two sinusoids (1000Hz + 15000 Hz)
sample_rate = 48000; nsamples = 256; F = [1 15] * 1000; A = [1 0.5]; % Time vector - use colon operator to generate integer vector of sample % numbers t = (0:nsamples-1) / sample_rate; % Test signal - use matrix notation to compose it with single expression signal = A * sin(2*pi*F'*t);
FIR filter¶
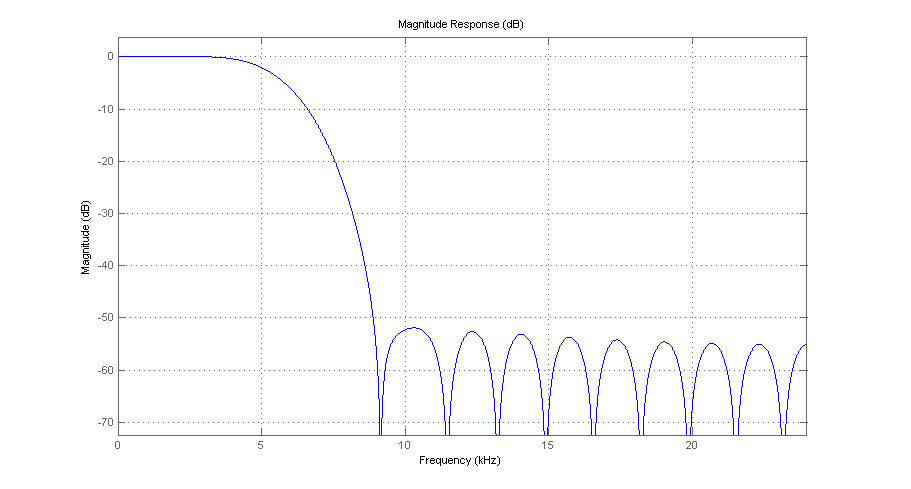
Assume a lowpass filter with cutoff frequency of 6 kHz. The expectation is this should filter out the 15 kHz component from the test signal
% Choose filter cutoff frequency (6 kHz) cutoff_hz = 6000; % Normalize cutoff frequency (wrt Nyquist frequency) nyq_freq = sample_rate / 2; cutoff_norm = cutoff_hz / nyq_freq; % FIR filter order (i.e. number of coefficients - 1) order = 28; % Create lowpass FIR filter through a direct approach: provide % (normalized) cutoff frequency and filter order (assumed as known). % fir1 takes care of designing the filter by imposing the constraints in % the frequency domain and transforming back to time using a given window % (the dafault used here is the Hamming window). % For more advanced requirements see e.g. firpmord and firpm % NOTE: fir1, firpmord and firpm all require Signal Processing Toolbox fir_coeff = fir1(order, cutoff_norm); % Analyse the filter using the Filter Visualization Tool fvtool(fir_coeff, 'Fs', sample_rate) % Filter the signal with the FIR filter filtered_signal = filter(fir_coeff, 1, signal);
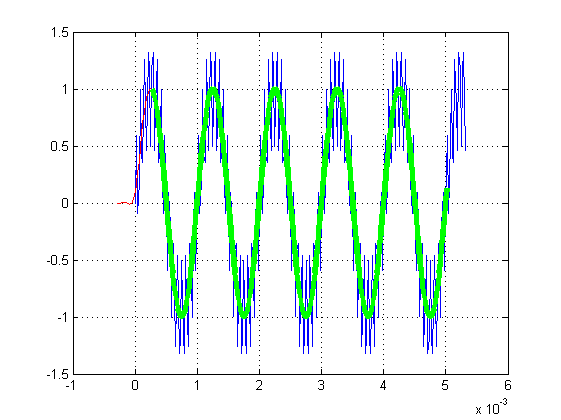
Plot the Signals¶
Also align filtered signal with original and discard transient samples (in this case the first order samples)
% Group delay as a scalar, in number of samples
group_delay = median(grpdelay(fir_coeff));
% Group delay in seconds
group_delay_s = group_delay / sample_rate;
% Plot the original signal...
figure(1)
plot(t, signal)
% ...and allow adding more plots
hold on
% Align and plot the filtered signal
% (On top of existing one)
plot(t-group_delay_s, filtered_signal, 'r-')
% Align and plot only the d6esired part of the filtered signal (discarding
% the transient)
plot(t(order:end)-group_delay_s, filtered_signal(order:end), ...
'g', 'LineWidth', 4);
grid on
hold off
Code Generation¶
Diplay C-like definitions for available data as a single-line strings
function outcstr = vectorToCDefFloat32_t( ...
cvarname, values_double)
% Fixed format parameters
typeString = 'float32_t';
valuesPerRow = 5;
% Number of values in the vector provided
nvalues = numel(values_double);
% Number of rows with numeric values in C expression
nrows = ceil(nvalues/valuesPerRow);
% Convert values to single-precision floating point
values_single = single(values_double);
% String creation, step 1 - data type, qualifier, length ...
outcstr = sprintf('const %s %s[%d] \t= {\n', ...
typeString, cvarname, numel(values_single));
% String creation, step 2 - numeric values, row by row
for k = 1:nrows
outcstr = [outcstr, sprintf('\t')]; %#ok<AGROW>
for h = 1:valuesPerRow
idx = (k-1)*valuesPerRow + h;
if(idx <= nvalues)
outcstr = [outcstr, sprintf('%+.10ff, ', values_single(idx))]; %#ok<AGROW>
else
outcstr = [outcstr, sprintf('\b\b')]; %#ok<AGROW>
break
end
end
outcstr = [outcstr, sprintf('\n')]; %#ok<AGROW>
end
% String creation, step 3 - end vector
outcstr = [outcstr, sprintf('};\n')];
% --- Helper function
function outstr = append(instr, extrastr)
outstr = [instr, sprintf(extrastr)];
% Use custom helper function vectorToCDefFloat32_t on filter coefficients, % initial test signal and filtered signal, respectively disp(vectorToCDefFloat32_t( 'fir_coeff', fir_coeff) ) disp(vectorToCDefFloat32_t( 'signal', signal) ) disp(vectorToCDefFloat32_t( 'filtered_signal', filtered_signal) )Manually export available data to C expressions
const float32_t fir_coeff[29] = {
-0.0018225231f, -0.0015879293f, +0.0000000000f, +0.0036977509f, +0.0080754301f,
+0.0085302219f, -0.0000000000f, -0.0173976980f, -0.0341458619f, -0.0333591551f,
+0.0000000000f, +0.0676308423f, +0.1522061825f, +0.2229246944f, +0.2504960895f,
+0.2229246944f, +0.1522061825f, +0.0676308423f, +0.0000000000f, -0.0333591551f,
-0.0341458619f, -0.0173976980f, -0.0000000000f, +0.0085302219f, +0.0080754301f,
+0.0036977509f, +0.0000000000f, -0.0015879293f, -0.0018225231f
};
const float32_t signal[256] = {
+0.0000000000f, +0.5924659371f, -0.0947343484f, +0.1913417131f, +1.0000000000f,
+0.4174197018f, +0.3535533845f, +1.2552931309f, +0.8660253882f, +0.4619397521f,
+1.3194792271f, +1.1827865839f, +0.5000000000f, +1.1827865839f, +1.3194792271f,
+0.4619397521f, +0.8660253882f, +1.2552931309f, +0.3535533845f, +0.4174197018f,
+1.0000000000f, +0.1913417131f, -0.0947343484f, +0.5924659371f, -0.0000000000f,
-0.5924659371f, +0.0947343484f, -0.1913417131f, -1.0000000000f, -0.4174197018f,
-0.3535533845f, -1.2552931309f, -0.8660253882f, -0.4619397521f, -1.3194792271f,
-1.1827865839f, -0.5000000000f, -1.1827865839f, -1.3194792271f, -0.4619397521f,
-0.8660253882f, -1.2552931309f, -0.3535533845f, -0.4174197018f, -1.0000000000f,
-0.1913417131f, +0.0947343484f, -0.5924659371f, +0.0000000000f, +0.5924659371f,
-0.0947343484f, +0.1913417131f, +1.0000000000f, +0.4174197018f, +0.3535533845f,
+1.2552931309f, +0.8660253882f, +0.4619397521f, +1.3194792271f, +1.1827865839f,
+0.5000000000f, +1.1827865839f, +1.3194792271f, +0.4619397521f, +0.8660253882f,
+1.2552931309f, +0.3535533845f, +0.4174197018f, +1.0000000000f, +0.1913417131f,
-0.0947343484f, +0.5924659371f, +0.0000000000f, -0.5924659371f, +0.0947343484f,
-0.1913417131f, -1.0000000000f, -0.4174197018f, -0.3535533845f, -1.2552931309f,
-0.8660253882f, -0.4619397521f, -1.3194792271f, -1.1827865839f, -0.5000000000f,
-1.1827865839f, -1.3194792271f, -0.4619397521f, -0.8660253882f, -1.2552931309f,
-0.3535533845f, -0.4174197018f, -1.0000000000f, -0.1913417131f, +0.0947343484f,
-0.5924659371f, +0.0000000000f, +0.5924659371f, -0.0947343484f, +0.1913417131f,
+1.0000000000f, +0.4174197018f, +0.3535533845f, +1.2552931309f, +0.8660253882f,
+0.4619397521f, +1.3194792271f, +1.1827865839f, +0.5000000000f, +1.1827865839f,
+1.3194792271f, +0.4619397521f, +0.8660253882f, +1.2552931309f, +0.3535533845f,
+0.4174197018f, +1.0000000000f, +0.1913417131f, -0.0947343484f, +0.5924659371f,
+0.0000000000f, -0.5924659371f, +0.0947343484f, -0.1913417131f, -1.0000000000f,
-0.4174197018f, -0.3535533845f, -1.2552931309f, -0.8660253882f, -0.4619397521f,
-1.3194792271f, -1.1827865839f, -0.5000000000f, -1.1827865839f, -1.3194792271f,
-0.4619397521f, -0.8660253882f, -1.2552931309f, -0.3535533845f, -0.4174197018f,
-1.0000000000f, -0.1913417131f, +0.0947343484f, -0.5924659371f, -0.0000000000f,
+0.5924659371f, -0.0947343484f, +0.1913417131f, +1.0000000000f, +0.4174197018f,
+0.3535533845f, +1.2552931309f, +0.8660253882f, +0.4619397521f, +1.3194792271f,
+1.1827865839f, +0.5000000000f, +1.1827865839f, +1.3194792271f, +0.4619397521f,
+0.8660253882f, +1.2552931309f, +0.3535533845f, +0.4174197018f, +1.0000000000f,
+0.1913417131f, -0.0947343484f, +0.5924659371f, -0.0000000000f, -0.5924659371f,
+0.0947343484f, -0.1913417131f, -1.0000000000f, -0.4174197018f, -0.3535533845f,
-1.2552931309f, -0.8660253882f, -0.4619397521f, -1.3194792271f, -1.1827865839f,
-0.5000000000f, -1.1827865839f, -1.3194792271f, -0.4619397521f, -0.8660253882f,
-1.2552931309f, -0.3535533845f, -0.4174197018f, -1.0000000000f, -0.1913417131f,
+0.0947343484f, -0.5924659371f, +0.0000000000f, +0.5924659371f, -0.0947343484f,
+0.1913417131f, +1.0000000000f, +0.4174197018f, +0.3535533845f, +1.2552931309f,
+0.8660253882f, +0.4619397521f, +1.3194792271f, +1.1827865839f, +0.5000000000f,
+1.1827865839f, +1.3194792271f, +0.4619397521f, +0.8660253882f, +1.2552931309f,
+0.3535533845f, +0.4174197018f, +1.0000000000f, +0.1913417131f, -0.0947343484f,
+0.5924659371f, +0.0000000000f, -0.5924659371f, +0.0947343484f, -0.1913417131f,
-1.0000000000f, -0.4174197018f, -0.3535533845f, -1.2552931309f, -0.8660253882f,
-0.4619397521f, -1.3194792271f, -1.1827865839f, -0.5000000000f, -1.1827865839f,
-1.3194792271f, -0.4619397521f, -0.8660253882f, -1.2552931309f, -0.3535533845f,
-0.4174197018f, -1.0000000000f, -0.1913417131f, +0.0947343484f, -0.5924659371f,
-0.0000000000f, +0.5924659371f, -0.0947343484f, +0.1913417131f, +1.0000000000f,
+0.4174197018f, +0.3535533845f, +1.2552931309f, +0.8660253882f, +0.4619397521f,
+1.3194792271f, +1.1827865839f, +0.5000000000f, +1.1827865839f, +1.3194792271f,
+0.4619397521f
};
const float32_t filtered_signal[256] = {
+0.0000000000f, -0.0010797828f, -0.0007681386f, -0.0001982932f, +0.0000644313f,
+0.0020854271f, +0.0036891871f, +0.0015855941f, -0.0026280805f, -0.0075907656f,
-0.0119390534f, -0.0086665964f, +0.0088981204f, +0.0430539288f, +0.0974468738f,
+0.1740405560f, +0.2681416571f, +0.3747720122f, +0.4893362224f, +0.6024154425f,
+0.7058740854f, +0.7968348861f, +0.8715901971f, +0.9277881384f, +0.9682182670f,
+0.9934674501f, +1.0012052059f, +0.9925859571f, +0.9681538343f, +0.9257026911f,
+0.8679010272f, +0.7952492833f, +0.7085021734f, +0.6100062132f, +0.5012753010f,
+0.3834386170f, +0.2592435479f, +0.1309866309f, -0.0000000000f, -0.1309866309f,
-0.2592435479f, -0.3834386170f, -0.5012753010f, -0.6100062132f, -0.7085021734f,
-0.7952492833f, -0.8679010272f, -0.9257026911f, -0.9681538343f, -0.9936656952f,
-1.0019733906f, -0.9936656952f, -0.9681538343f, -0.9257026911f, -0.8679010272f,
-0.7952492833f, -0.7085021734f, -0.6100062132f, -0.5012753010f, -0.3834386170f,
-0.2592435479f, -0.1309866309f, +0.0000000000f, +0.1309866309f, +0.2592435479f,
+0.3834386170f, +0.5012753010f, +0.6100062132f, +0.7085021734f, +0.7952492833f,
+0.8679010272f, +0.9257026911f, +0.9681538343f, +0.9936656952f, +1.0019733906f,
+0.9936656952f, +0.9681538343f, +0.9257026911f, +0.8679010272f, +0.7952492833f,
+0.7085021734f, +0.6100062132f, +0.5012753010f, +0.3834386170f, +0.2592435479f,
+0.1309866309f, -0.0000000000f, -0.1309866309f, -0.2592435479f, -0.3834386170f,
-0.5012753010f, -0.6100062132f, -0.7085021734f, -0.7952492833f, -0.8679010272f,
-0.9257026911f, -0.9681538343f, -0.9936656952f, -1.0019733906f, -0.9936656952f,
-0.9681538343f, -0.9257026911f, -0.8679010272f, -0.7952492833f, -0.7085021734f,
-0.6100062132f, -0.5012753010f, -0.3834386170f, -0.2592435479f, -0.1309866309f,
+0.0000000000f, +0.1309866309f, +0.2592435479f, +0.3834386170f, +0.5012753010f,
+0.6100062132f, +0.7085021734f, +0.7952492833f, +0.8679010272f, +0.9257026911f,
+0.9681538343f, +0.9936656952f, +1.0019733906f, +0.9936656952f, +0.9681538343f,
+0.9257026911f, +0.8679010272f, +0.7952492833f, +0.7085021734f, +0.6100062132f,
+0.5012753010f, +0.3834386170f, +0.2592435479f, +0.1309866309f, +0.0000000000f,
-0.1309866309f, -0.2592435479f, -0.3834386170f, -0.5012753010f, -0.6100062132f,
-0.7085021734f, -0.7952492833f, -0.8679010272f, -0.9257026911f, -0.9681538343f,
-0.9936656952f, -1.0019733906f, -0.9936656952f, -0.9681538343f, -0.9257026911f,
-0.8679010272f, -0.7952492833f, -0.7085021734f, -0.6100062132f, -0.5012753010f,
-0.3834386170f, -0.2592435479f, -0.1309866309f, +0.0000000000f, +0.1309866309f,
+0.2592435479f, +0.3834386170f, +0.5012753010f, +0.6100062132f, +0.7085021734f,
+0.7952492833f, +0.8679010272f, +0.9257026911f, +0.9681538343f, +0.9936656952f,
+1.0019733906f, +0.9936656952f, +0.9681538343f, +0.9257026911f, +0.8679010272f,
+0.7952492833f, +0.7085021734f, +0.6100062132f, +0.5012753010f, +0.3834386170f,
+0.2592435479f, +0.1309866309f, -0.0000000000f, -0.1309866309f, -0.2592435479f,
-0.3834386170f, -0.5012753010f, -0.6100062132f, -0.7085021734f, -0.7952492833f,
-0.8679010272f, -0.9257026911f, -0.9681538343f, -0.9936656952f, -1.0019733906f,
-0.9936656952f, -0.9681538343f, -0.9257026911f, -0.8679010272f, -0.7952492833f,
-0.7085021734f, -0.6100062132f, -0.5012753010f, -0.3834386170f, -0.2592435479f,
-0.1309866309f, +0.0000000000f, +0.1309866309f, +0.2592435479f, +0.3834386170f,
+0.5012753010f, +0.6100062132f, +0.7085021734f, +0.7952492833f, +0.8679010272f,
+0.9257026911f, +0.9681538343f, +0.9936656952f, +1.0019733906f, +0.9936656952f,
+0.9681538343f, +0.9257026911f, +0.8679010272f, +0.7952492833f, +0.7085021734f,
+0.6100062132f, +0.5012753010f, +0.3834386170f, +0.2592435479f, +0.1309866309f,
+0.0000000000f, -0.1309866309f, -0.2592435479f, -0.3834386170f, -0.5012753010f,
-0.6100062132f, -0.7085021734f, -0.7952492833f, -0.8679010272f, -0.9257026911f,
-0.9681538343f, -0.9936656952f, -1.0019733906f, -0.9936656952f, -0.9681538343f,
-0.9257026911f, -0.8679010272f, -0.7952492833f, -0.7085021734f, -0.6100062132f,
-0.5012753010f, -0.3834386170f, -0.2592435479f, -0.1309866309f, -0.0000000000f,
+0.1309866309f
};
mbed-dsp library¶
Import librarymbed-dsp
CMSIS DSP library
CMSIS DSP API¶
Import program
00001 #include "arm_math.h" 00002 #include "math_helper.h" 00003 #include <stdio.h> 00004 00005 #define BLOCK_SIZE 32 00006 #define NUM_BLOCKS 10 00007 00008 #define TEST_LENGTH_SAMPLES (BLOCK_SIZE * NUM_BLOCKS) 00009 00010 #define SNR_THRESHOLD_F32 140.0f 00011 #define NUM_TAPS 29 00012 00013 /* ------------------------------------------------------------------- 00014 * The input signal and reference output (computed with MATLAB) 00015 * are defined externally in arm_fir_lpf_data.c. 00016 * ------------------------------------------------------------------- */ 00017 extern float32_t testInput_f32_1kHz_15kHz[TEST_LENGTH_SAMPLES]; 00018 extern float32_t refOutput[TEST_LENGTH_SAMPLES]; 00019 00020 /* ------------------------------------------------------------------- 00021 * Declare State buffer of size (numTaps + blockSize - 1) 00022 * ------------------------------------------------------------------- */ 00023 static float32_t firStateF32[BLOCK_SIZE + NUM_TAPS - 1]; 00024 00025 /* ---------------------------------------------------------------------- 00026 * FIR Coefficients buffer generated using fir1() MATLAB function. 00027 * fir1(28, 6/24) 00028 * ------------------------------------------------------------------- */ 00029 const float32_t firCoeffs32[NUM_TAPS] = { 00030 -0.0018225230f, -0.0015879294f, +0.0000000000f, +0.0036977508f, +0.0080754303f, 00031 +0.0085302217f, -0.0000000000f, -0.0173976984f, -0.0341458607f, -0.0333591565f, 00032 +0.0000000000f, +0.0676308395f, +0.1522061835f, +0.2229246956f, +0.2504960933f, 00033 +0.2229246956f, +0.1522061835f, +0.0676308395f, +0.0000000000f, -0.0333591565f, 00034 -0.0341458607f, -0.0173976984f, -0.0000000000f, +0.0085302217f, +0.0080754303f, 00035 +0.0036977508f, +0.0000000000f, -0.0015879294f, -0.0018225230f 00036 }; 00037 00038 /* ---------------------------------------------------------------------- 00039 * FIR LPF Example 00040 * ------------------------------------------------------------------- */ 00041 int32_t main(void) { 00042 /* Call FIR init function to initialize the instance structure. */ 00043 arm_fir_instance_f32 S; 00044 arm_fir_init_f32(&S, NUM_TAPS, (float32_t *)&firCoeffs32[0], &firStateF32[0], BLOCK_SIZE); 00045 00046 /* ---------------------------------------------------------------------- 00047 * Call the FIR process function for every blockSize samples 00048 * ------------------------------------------------------------------- */ 00049 for (uint32_t i=0; i < NUM_BLOCKS; i++) { 00050 float32_t* signal = testInput_f32_1kHz_15kHz + (i * BLOCK_SIZE); 00051 arm_fir_f32(&S, signal, signal, BLOCK_SIZE); 00052 } 00053 00054 /* ---------------------------------------------------------------------- 00055 * Compare the generated output against the reference output computed 00056 * in MATLAB. 00057 * ------------------------------------------------------------------- */ 00058 float32_t snr = arm_snr_f32(refOutput, testInput_f32_1kHz_15kHz, TEST_LENGTH_SAMPLES); 00059 printf("snr: %f\n\r", snr); 00060 if (snr < SNR_THRESHOLD_F32) { 00061 printf("Failed\n\r"); 00062 } else { 00063 printf("Success\n\r"); 00064 } 00065 }
mbed DSP API¶
Import program
00001 #include "mbed.h" 00002 #include "dsp.h" 00003 00004 #define BLOCK_SIZE (32) 00005 #define NUM_BLOCKS (10) 00006 #define TEST_LENGTH_SAMPLES (BLOCK_SIZE * NUM_BLOCKS) 00007 00008 #define SAMPLE_RATE (48000) 00009 00010 #define SNR_THRESHOLD_F32 (50.0f) 00011 00012 float32_t expected_output[TEST_LENGTH_SAMPLES]; 00013 float32_t output[TEST_LENGTH_SAMPLES]; 00014 00015 /* FIR Coefficients buffer generated using fir1() MATLAB function: fir1(28, 6/24) */ 00016 #define NUM_TAPS 29 00017 const float32_t firCoeffs32[NUM_TAPS] = { 00018 -0.0018225230f, -0.0015879294f, +0.0000000000f, +0.0036977508f, +0.0080754303f, 00019 +0.0085302217f, -0.0000000000f, -0.0173976984f, -0.0341458607f, -0.0333591565f, 00020 +0.0000000000f, +0.0676308395f, +0.1522061835f, +0.2229246956f, +0.2504960933f, 00021 +0.2229246956f, +0.1522061835f, +0.0676308395f, +0.0000000000f, -0.0333591565f, 00022 -0.0341458607f, -0.0173976984f, -0.0000000000f, +0.0085302217f, +0.0080754303f, 00023 +0.0036977508f, +0.0000000000f, -0.0015879294f, -0.0018225230f 00024 }; 00025 #define WARMUP (NUM_TAPS-1) 00026 #define DELAY (WARMUP/2) 00027 00028 int main() { 00029 Sine_f32 sine_1KHz( 1000, SAMPLE_RATE, 1.0); 00030 Sine_f32 sine_15KHz(15000, SAMPLE_RATE, 0.5); 00031 FIR_f32<NUM_TAPS> fir(firCoeffs32); 00032 00033 float32_t buffer_a[BLOCK_SIZE]; 00034 float32_t buffer_b[BLOCK_SIZE]; 00035 for (float32_t *sgn=output; sgn<(output+TEST_LENGTH_SAMPLES); sgn += BLOCK_SIZE) { 00036 sine_1KHz.generate(buffer_a); // Generate a 1KHz sine wave 00037 sine_15KHz.process(buffer_a, buffer_b); // Add a 15KHz sine wave 00038 fir.process(buffer_b, sgn); // FIR low pass filter: 6KHz cutoff 00039 } 00040 00041 sine_1KHz.reset(); 00042 for (float32_t *sgn=expected_output; sgn<(expected_output+TEST_LENGTH_SAMPLES); sgn += BLOCK_SIZE) { 00043 sine_1KHz.generate(sgn); // Generate a 1KHz sine wave 00044 } 00045 00046 float snr = arm_snr_f32(&expected_output[DELAY-1], &output[WARMUP-1], TEST_LENGTH_SAMPLES-WARMUP); 00047 printf("snr: %f\n\r", snr); 00048 if (snr < SNR_THRESHOLD_F32) { 00049 printf("Failed\n\r"); 00050 } else { 00051 printf("Success\n\r"); 00052 } 00053 }
