Dead Reckoning
In this tutorial, we show you how to take readings from a digital accelerometer and compass, and then combine them to form a rudimentary dead reckoning system.
Hardware Components
For this example we use:
- an mbed!
- An ADXL345 accelerometer
- ADXL345
- ADXL345 SparkFun Breakout Board
- An HMC6352 compass
- HMC6352
- HMC6352 SparkFun Breakout Board
- A breadboard, some wires and a battery pack
Software Components
To drive these hardware components, we use the following libraries
- ADXL345 library
- HMC6352 library
- Dead Reckoning Demo library
Hardware
(hand written schematic image)
First of all, plug your mbed into the breadboard. Connect the GND pin with the breadboard's ground line and the VOUT pin to the power line.
ADXL345
- Connect the GND pin to the ground line on the breadboard
- Connect the VCC pin to the power line
- Connect the CS pin to p8 on the mbed (used as DigitalOut)
- Connect the SDO pin to p6 on the mbed (used as SPI miso)
- Connect the SDA pin to p5 on the mbed (used as SPI mosi)
- Connect the SCL pin to p7 on the mbed (used as SPI sck)
HMC6352
- Connect the GND pin to the ground line on the breadboard
- Connect the VCC pin to the power line on the breadboard
- Connect the SDA pin to p28 on the mbed (used as I2C sda)
- Connect the SCL pin to p27 on the mbed (used as I2C scl)
Battery Pack
- Connect the negative terminal wire to the GND pin on the mbed
- Connect the positive terminal wire to the VIN pin on the mbed
(image of mbed + components + wires connected in breadboard)
Software
The full program including the libraries is published here:
Dead Reckoning Demo
Here is the main function from the demo code:
//Dead Reckoning Demo.
#include "deadReckoning.h"
#define END_TIME 15 //Seconds.
deadReckoning reckon(p5, p6, p7, p8, p28, p27);
DigitalOut led1(LED1); //Keep LED on while the program is running.
Serial pc(USBTX, USBRX);
Timeout timeout;
LocalFileSystem local("local");
FILE* fp;
//Close the current file and exit the program.
void endSample(void) {
led1 = 0;
fclose(fp);
exit(0);
}
int main() {
led1 = 1;
timeout.attach(&endSample, END_TIME);
fp = fopen("/local/results.csv", "w");
while (1) {
wait(0.05);
fprintf(fp, "%f, %f\n", reckon.getAcceleration(),
reckon.getHeading());
}
} What is "Dead Reckoning"?
Dead reckoning is estimating your current position by using a pre-determined start point, and then updating your position estimate through knowledge of your speed over time, and the direction you're facing.
Each new estimate is calculated from old estimates - so if you have even a tiny error to begin, it won't take long before it grows out of proportion! While our system will never be 100% accurate because of this, we will still be able to get a sensible fix on our position using this technique.
How do we do it?
One way is to use a sensor called an accelerometer which measures acceleration relative to free fall or 'proper acceleration'; if we pushed an accelerometer along a table about half a metre, took readings of its outputs (converting the units to m/s^2) and plotted them on an acceleration-time graph, we would get something that looks like this:
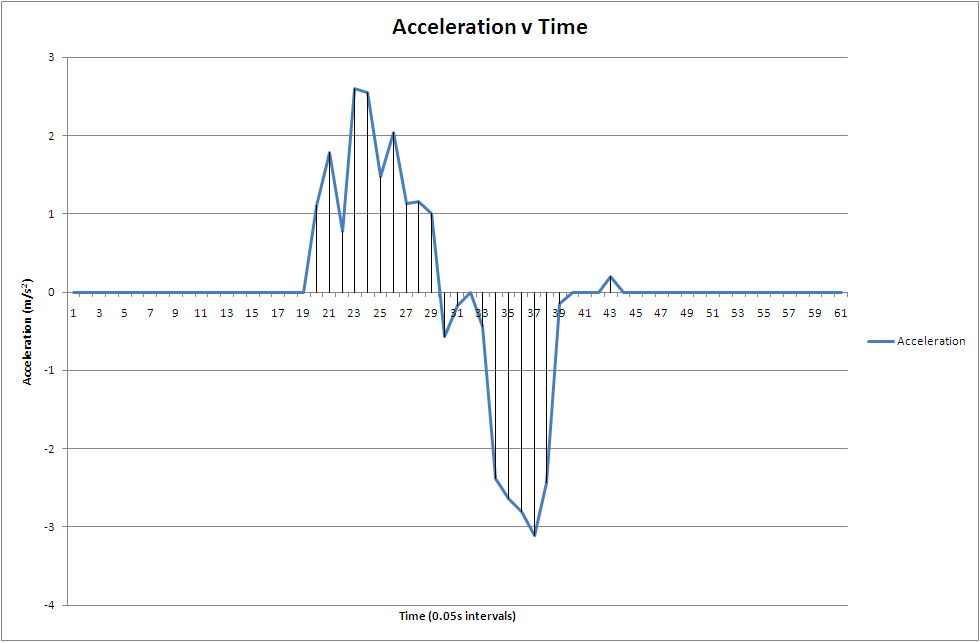
The area under this curve is equal to the velocity of the accelerometer. Therefore if we were to integrate the acceleration we observed and plot the results on a velocity-time graph, we would get something that looks like this:
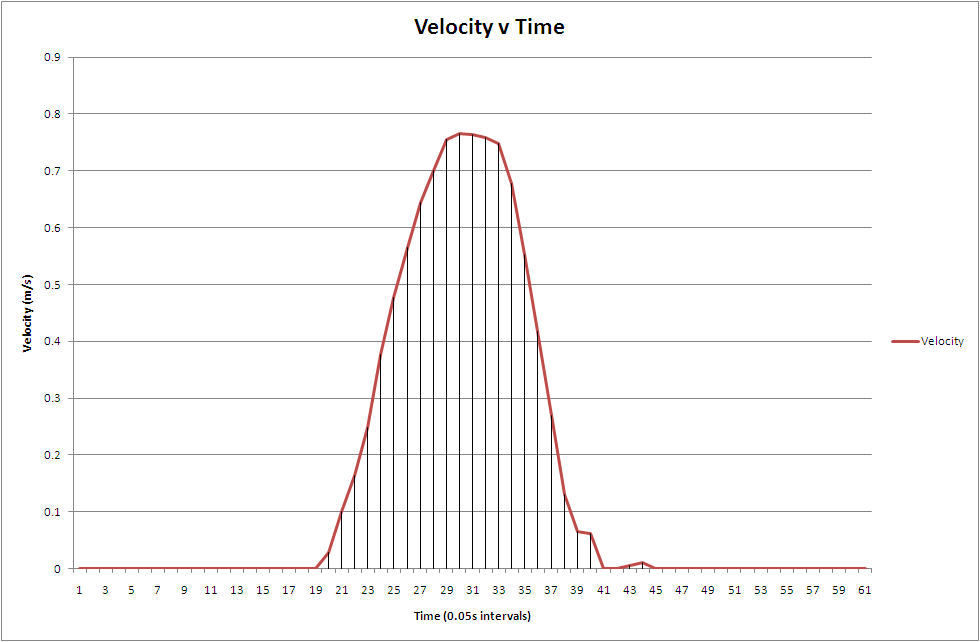
Finally, the area under this curve is equal to the displacement of the accelerometer, and if we integrate the velocity we calculated and plotted it on a displacement-time, we would get something that looks like this:
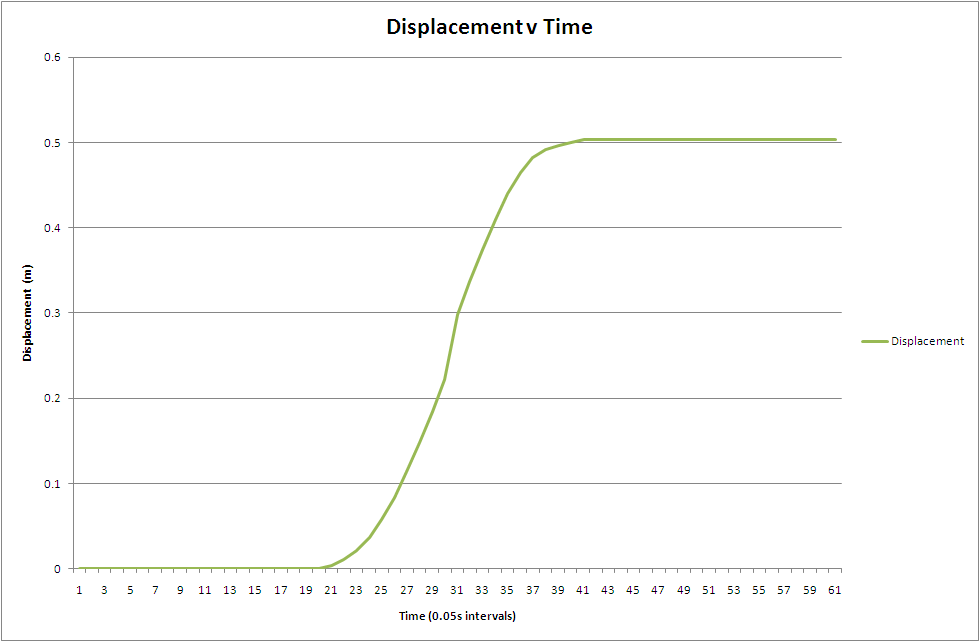
This graph represents our position estimate over time, which was obtained by integrating the output of the accelerometer twice.
Getting from accelerometer readings to displacement
Now we'll explain how to go from sampling your accelerometer to estimating your current position.
The ADXL345 which we have used in this example, is a triple axis accelerometer with a digital interface; that means it can sense acceleration in all three axes in 3D space, and we sample it by sending a command over a serial digital protocol such as SPI which returns a number relating to the acceleration in terms of g-force. This is opposed to an analog accelerometer which is sampled by reading a voltage off one of its pins that is proportional to the acceleration.
The ADXL345 library contains the required methods to sample the accelerometer and an example of how to use them.
1. Setup the accelerometer
The accelerometer is first placed in standby mode so it can accept changes to its configuration. It is set the highest resolution (13-bit sign extended values with 3.9mg/LSB sensitivity), and the fastest data rate (3.2kHz). Finally it is placed into measurement mode where it continuously updates the acceleration values in its registers at the specified data rate.
//Accelerometer initialisation.
//Go into standby mode to configure the device.
accelerometer->setPowerControl(0x00);
//Full resolution, +/-16g, 4mg/LSB.
accelerometer->setDataFormatControl(0x0B);
//3.2kHz data rate.
accelerometer->setDataRate(ADXL345_3200HZ);
//Measurement mode.
accelerometer->setPowerControl(0x08); 2. Calibrate the accelerometer
Unfortunately, accelerometers are prone to inaccuracies, including offset errors. This when they read an acceleration value which is not equal to zero, despite not moving. One way to get round this, is to calculate a bias. We do this by taking a certain number of calibration readings, before we start our displacement calculations, and averaging them. The accelerometer must be perfectly still while this is done. By subtracting this bias from all the subsequent readings take we will have ensured all the readings are centred around what we believe is the 0g value (the reading the accelerometer should show when it is perpindicular to the local gravity vector, and not moving).
int xAccumulator = 0;
int calibrationCount = 0;
while (calibrationCount < CALIBRATION_COUNT) {
//Make sure the accelerometer has had enough time
//to take a new sample.
wait(ACC_SAMPLE_PERIOD);
accelerometer->getOutput(accelerometerReadings);
xAccumulator += (int16_t)accelerometerReadings[0];
calibrationCount++;
}
xBias = xAccumulator / CALIBRATION_COUNT; 3. Sampling the accelerometer
An update method is attached to a Ticker and is called at a rate small enough to allow the necessary time to sample the accelerometer and perform the calculations for position estimation.
At the start of the update method, the accelerometer is sampled by taking a set number of readings and averaging them. Accelerometers are quite noisy, and averaging values will help in reducing the error introduced by the noise.
int xAccumulator = 0;
int sampleCount = 0;
//We'll take a certain number of samples and then average them,
//to try and reduce some of the noise.
while (sampleCount < SAMPLE_COUNT) {
//Make sure the accelerometer has had enough time
//to take a new sample.
wait(ACC_SAMPLE_PERIOD);
accelerometer->getOutput(accelerometerReadings);
//16 bit, sign extended values.
xAccumulator += (int16_t)accelerometerReadings[0];
sampleCount++;
}
xAcceleration = xAccumulator / SAMPLE_COUNT; 4. Removing the offset
The 0g offset, calculated in calibration is then removed from this averaged value.
//Remove 0g offset.
xAcceleration -= xBias; 5. Window of discrimination
Even after we average several readings and remove the offset, there might still be some jitter around the stationary value; we can attempt to deal with this by providing a window of discrimination between valid and invalid readings. By observing the readings from the accelerometer while it is stationary we can set sensible minimum and maximum for this window. If our reading falls within these limits we can assume we're just seeing noise and appropriately set the acceleration to zero.
However, if the reading falls outside these limits, we can assume we're observing "real" acceleration. If this is the case we'll scale the value we've read to m/s^2 by mulitiplying by the gain, or sensitivity. In the case of the ADXL345, the datasheet claims the typical scale factor is 3.9mg/LSB at full resolution. With the appropriate equipment, you can calculate the sensitivity for your particular sensor (as they can vary immensely between the same models) but that is outside the scope of this tutorial, since we can assume the typical specification is "good enough" for our application. For more information about this topic please see http://www.vectornav.com/calibration#accelerometer.
//There will be a certain amount of noise around 0 which would give
//false acceleration readings. If the acceleration value falls within
//a certain band, we can assume it's just noise and set the actual
//acceleration to 0.
if (xAcceleration >= X_WINDOW_MIN && xAcceleration <= X_WINDOW_MAX) {
xAcceleration = 0;
}
//If we're sure we're seeing actual acceleration, then we'll convert it
//to m/s^2.
else{
xAcceleration *= X_GAIN;
} 6. Double Integration
(trapezoid method picture)
We can simplify things by considering the area under the curve between two points as being made up of a rectangle with a triangle sitting on top of it. The area of the rectangle is:
Sample(n-1) * t
The area of the triangle is:
(Sample(n) - Sample(n-1)) * 0.5 * t
If we add the two together we have a value of the integral for this time period.
By applying this to our acceleration readings, and then again to our velocity calculations, we can get an estimate of position.
//First x-axis integration.
xVelocity = prev_xVelocity +
(prev_xAcceleration +
((xAcceleration - prev_xAcceleration)/2.0))*UPDATE_TIME;
//Second x-axis integration.
xPosition = prev_xPosition +
(prev_xVelocity +
((xVelocity - prev_xVelocity)/2.0))*UPDATE_TIME; 7. Checking for the end of movement
We know our accelerometer can give out noisy values and this presents a problem when considering velocity calculations. If we move our accelerometer from a stationary point a certain distance and then bring it to rest again, we should get an equal and opposite amount of acceleration in both directions. If we don't read an equal amount, our velocity will remain constant at a number since it wasn't brought back to zero by an equal and opposite acceleration, and being stationary, the acceleration will simply read zero providing no change in velocity.
We can fix this by checking how many zero readings of acceleration we've had in a row. If we've had a certain number, we can make a pretty good assumption that our accelerometer has been brought to rest and can set the velocity to zero.
//If we've observed no acceleration in the past N readings, we can assume
//movement has stopped, and can reset the velocity variables, greatly
//reducing position errors.
if(xAcceleration == 0){
noAccelerationCount++;
}
else{
noAccelerationCount = 0;
}
if(noAccelerationCount > NO_MOVEMENT){
xVelocity = 0.0;
prev_xVelocity = 0.0;
noAccelerationCount = 0;
} 8. Setting up for the next update
The last thing we need to do is set our previous value variables in order to make our calculations correct when the next update occurs.
prev_xAcceleration = xAcceleration;
prev_xVelocity = xVelocity;
prev_xPosition = xPosition; Getting the compass heading
Fortunately, the heading is a lot easier to determine than the position. The HMC6352 digital compass module spits out a number between 0 and 3599 (corresponding to 0 to 359.9 degrees) when it is sent the appropriate command in standby or query mode. In continuous mode, simply addressing the module will allow the reading of the heading.
It is initialised for continuous mode, sampling at the highest data rate (20Hz), with a periodic set/reset to minimise errors from magnetic fields that can throw off the readings.
//Continuous mode, periodic set/reset, 20Hz measurement rate.
compass->setOpMode(HMC6352_CONTINUOUS, 1, 20); In the update method, getting the current heading is as simple as:
//Update heading.
heading = compass->sample() / 10.0; References
Freescale Application Note - Implementing Positioning Algorithms Using Accelerometers
2 comments
You need to log in to post a comment



Thank you for this.
Could you please tell me how I can determine the angle and position of the HMC6352? I want to attache solar cell with it and would like to know the position when I change the angle of HMC6352.