E.R.I.C. Walking Gait
A gait is the manner or pattern that an animal's feet contact the ground during locomotion.
For E.R.I.C. I will approach this problem from a mathematical rather than empirical stand point. Logically for a biped the it stands to reason that when walking one leg will be in the air when the other in on the floor, and that the legs will follow the same motion. So mathematically the two legs will be anti-phase (180° phase shift) to one another.
For a quadruped this becomes more difficult.
Why is it more complex for a quadruped?
Because a biped's feet spend half the time in the air and half on the floor they can move at the same velocity in both the forward and return motion.
For a quadruped each leg spends 75% of its time in contact with the floor and only 25% of the time in the air. This means that to repeat the step pattern it needs to travel 3 times faster in the air then when on the floor. In short the velocity or step pattern is non linear, which adds complexity to the system.
Developing the gait
My first idea was to have a master clock that runs at a linear rate. I then plan to develop a formula that translates this into the non-linear clock / counter. This new clock / counter can then be used to control a leg in a non-linear manner.
Because all legs will still follow the same pattern this device can be phase shifted by 90° to calculate the position of the next leg, and phase shifted again for the position of the next leg, and so on.
In the end the gait should look something like the 'lateral walk sequence' in the diagram below.

Maths / code development
So to start with if the leg need to move backward 75% of the time then if the full cycle was 360° then this would equate to 270° going backward and 90° going forwards.
So if the master timer ran from 0 to 360 seconds then when the timer was <270 the rate would be 180°/270 seconds or 2/3° per second. For the remainder of the time the rate would be 180°/90 seconds or 2° per sec.
So the code that might implement this might look like...
if (master_timer < 270){
leg1_timer = master_timer * 2/3;
} else {
leg1_timer = (master_timer * 2) - 360;
}
The -360 bit has to be added because at 270 seconds we must be at 180°. However this can be cancelled out later on (see below).
For the second leg (which requires a 90° phase shift) the code could be...
master_timer += 90; // Add a 90° phase shift
if (master_timer > 360){
master_timer -= 360; // Stop the master_timer going out of bounds
}
if (master_timer < 270){
leg2_timer = master_timer * 2/3;
} else {
leg2_timer = (master_timer * 2) - 360;
}
The problem of the master_timer being greater than 360° is a situation I don't want so I added the line below the phase shift to stop it happening.
If the four leg timers were in an array then each leg could be calculated in a for loop, such as...
float leg_timer[4];
float time;
for( int i = 0; i < 4; i++){
time = master_time + (90 * i); // Add a phase shift
if (time > 360){
time -= 360; // Stop timer going out of bounds
}
if (time < 270){
leg_timer [i] = time * 2/3;
} else {
leg_timer [i] = (time * 2) - 360;
}
}
What next?
So I have a mechanism that will convert a linear timer into a non-linear set of controls for each leg, each of which is phase shifted from the last by 90°.
The position of the foot will move the perimeter of an ellipse at a rate controlled by the leg timer. This appears to be a common trend in robotics as seen here. The maths behind the ellipse pattern is shown in one of my other notebook pages.
The next thing to change is the timer. Really a 360 second cycle is a bit slow and just to work out the maths. All mbed trigonometry works in radians so the cycles should be 2π radians. Also I want some kind of cadence, that is a way to regulate the pace of the step in such a way that one complete cycle will last as long as I desire. Finally I want a way to control the length of the stride.
So I add in some code to do these things and print the results to the terminal. A graph showing the sequence of the feet lifting of the floor is shown below.
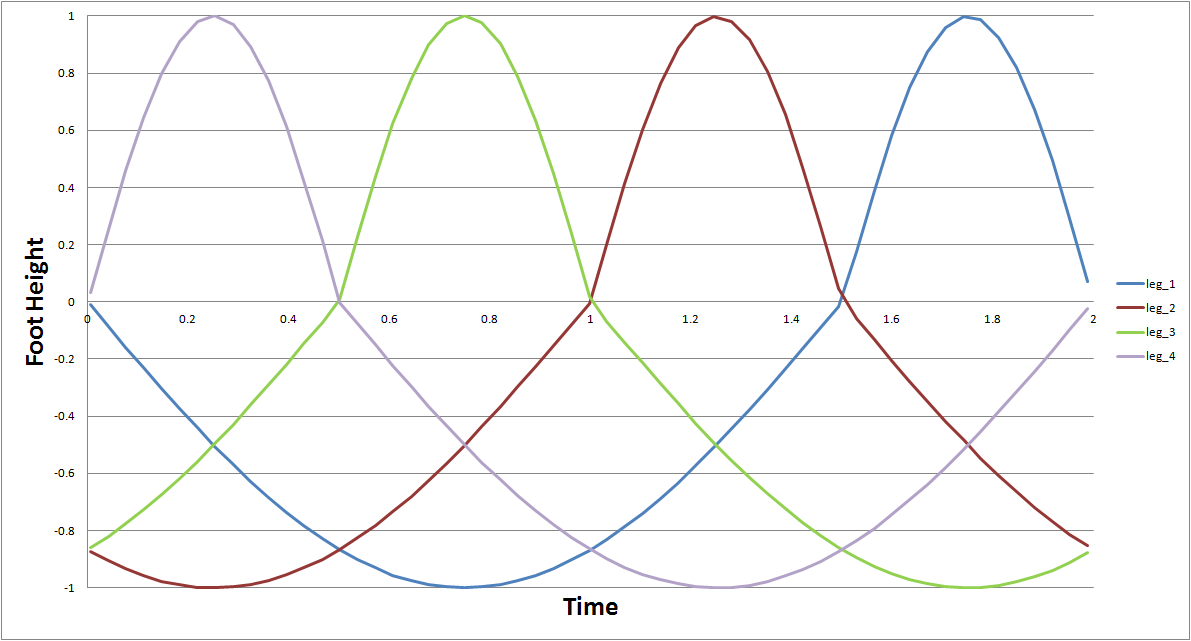
Cut to the chase
OK so it's time to wrap up everything into a full function. I add in the code to calculate the elliptical profile of the feet and add in a offset in the Z axis. The program wrapping it all up and allowing E.R.I.C. to take his first steps is here.
Import programERIC_Walking_4_Legs
E.R.I.C.'s first attempt to walk
And here is what happened when E.R.I.C. tried to walk...
OK so that was something of a disaster! E.R.I.C. fell over almost straight away.
What happened???
Well on closer inspection I think the reason that E.R.I.C. fell over is because his centre of gravity (COG) fell outside the triangle formed by the 3 legs that were on the ground.
This was probably made worst because mechanically E.R.I.C. is not finished yet, he has a head, body and battery pack to construct yet, so depending on where I put these he could become more stable. However I'm not prepared to accept this as a answer and hope it all works out.
So what are you going to do?
Well I think the secret to making E.R.I.C. more stable lays in the hips...
As the walking part will be deterministic (i.e. no rough terrain, no obstacles, no stairs, etc.) rather than write an algorithm that works out E.R.I.C.'s COG and shifts the body around it will achieve the same result with a maths formula.
I want the body to start over one side as the 1st leg moves, then move to the other side for the next 2 legs and finally back over again for the last leg. This is basically the cosine function. So I'll put in a constant value for the sideways shift and let the cosine function move the body in sympathy as it goes through it's walk cycle.
After a bit of experimentation I find that about 45 mm offsets the body nicely so E.R.I.C. can pick up any of his feet and not fall over. The downside is that it needs to shift the body weight over pretty quickly so it's there in time for the foot lift. So to do this I bump the constant up to 150 mm but put in some conditions that limit it to 45 mm max.
The result is shown in the video below.
This time the results are much better, E.R.I.C. doesn't fall over! So I guess I'm on to something. The motion is still very jerky and I would like to refine it to get it a lot smoother but its a good start.
Please log in to post comments.
